Populating Next Right Pointers in Each Node

https://leetcode.com/problems/populating-next-right-pointers-in-each-node/

Question

You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Follow up:

• You may only use constant extra space.

• Recursive approach is fine, you may assume implicit stack space does not count as extra space for this problem.

Example 1:

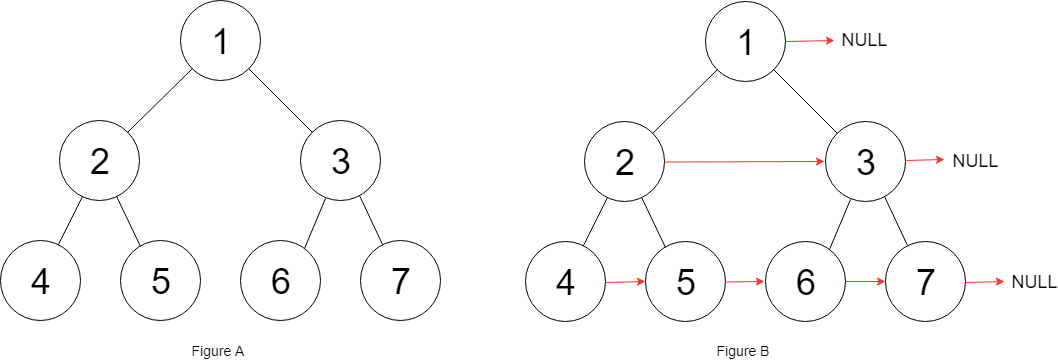
Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]
Explanation: Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

Answer

From here.

Simply do it level by level, using the next-pointers of the current level to go through the current level and set the next-pointers of the next level.

I say "real" O(1) space because of the many recursive solutions ignoring that recursion management needs space.

def connect(self, root):
    while root and root.left:
        next = root.left
        while root:
            root.left.next = root.right
            root.right.next = root.next and root.next.left
            root = root.next
        root = next